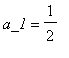 ,
, 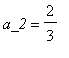 ,
, 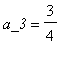 等等。一般項,或者第n項,則從公式
等等。一般項,或者第n項,則從公式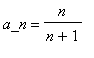 所獲得。
所獲得。 14 課: 數列簡介
數列是一個無窮的表單,是一個無窮個物件且依某些順序排列而成的集合。在這課程中,我們將會專門討論數字的數列。例如
1, 2, 3, 4, 5, 6, 7, ...
1, -1/3, 1/9, -1/27, 1/81, -1/243, ...
1/2, 2/3, 3/4, 4/5, 5/6, 6/7, ...
是三個由數字組成的數列。(注意 ... 符號,符號 ...代表這是無窮連續的表單)
我們代表性的以單一字母去表示數列;數列中個別項則以相同字母,在字母的下標位置表示出。例如,假如在下面最後的數列稱為a,則
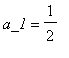 ,
, 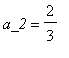 ,
, 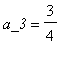 等等。一般項,或者第n項,則從公式
等等。一般項,或者第n項,則從公式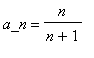 所獲得。
所獲得。
請問下面第二個數列中的一般項為何?
解: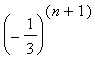 (為什麼指數是 n+1
且不只是 n ?)
(為什麼指數是 n+1
且不只是 n ?)
在Maple中有一個方法可以產生表單,就是使用金錢符號,$.
> n^2 $n=1..10;
![]()
> n/(n+1) $n=3..7;
![]()
注意在這裡使用 ‘list’比使用
‘sequence’好 ; Maple在這只產生有限項數的數字,而不是整個數列。儘管如此,這已經足夠讓我們從一個函數n去繪出一般項a_n而得到的數列圖。使用正確的語法,Maple中的plot指令將會幫我們做到。在下面的例子中,我們首先定義一列的點去繪出(
點
( n ,
a_n )),然後把這個表傳給plot。
> a := [[n, n^2] $n=1..10];
![]()
> plot(a, x=0..12, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences117.gif)
這數列a在
![]() 時,給了一張好的圖。下一個的例子是
時,給了一張好的圖。下一個的例子是
![]() 的第n項數列
。
的第n項數列
。
> b := [[n, n/(n+1)] $n=1..10];
![]()
> plot(b, x=0..12, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences123.gif)
注意到數列 a 與 數列 b 在 n 值極大時其表現出來十分的不同:數列 a 沒有界限的成長,而 b 看來好像接近一個有限的值。我們可以藉由繪出 更多的 b 值的圖去肯定這件事。
> plot([[n, n/(n+1)] $n=1..100], x=0..100, y=0..2, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences131.gif)
現在對那似乎更清楚了,當n值變大時,項數
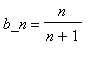 則愈接近1
。(這從代數學來看也應該很清楚:當n值非常大時,分母中的‘+1’將產生很小的差距,所以分數應該趨近於像當
則愈接近1
。(這從代數學來看也應該很清楚:當n值非常大時,分母中的‘+1’將產生很小的差距,所以分數應該趨近於像當
![]() 時。)在像數列b
的例子中,在n值變的很大時,它的一般項會接近一個固定且有限的數字L,則我們稱這數列 收斂 到L, 或者說有一個L的極限,所以我們寫成
時。)在像數列b
的例子中,在n值變的很大時,它的一般項會接近一個固定且有限的數字L,則我們稱這數列 收斂 到L, 或者說有一個L的極限,所以我們寫成
![]()
除此之外,我們則稱這數列為發散,或者極限不存在。例如,我們在下面看到的
>
從下列已知數列的表示式,以圖表表示出這數列的一般項,且定義它們是否收斂。假如收斂,試著找出它們的極限。(在畫圖之前,你可以試著猜猜答案;它們並不全都是明顯的。)
(a) 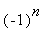 (b)
(b) 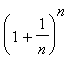 (c)
(c) 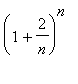 (d)
(d) 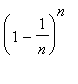
(e) ![]() (f)
(f) 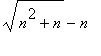 (g)
(g) ![]()
解.
> plot([[n, (-1)^n] $n=1..20], x=0..20, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences151.gif)
數列(a)不是收斂:項數在1和-1間前後跳躍,且不接近任何固定的值。
> plot([[n, (1 + 1/n)^n] $n=1..30], x=0..30, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences152.gif)
數列(b)出現在收斂到趨近2.7的一個極限值。(事實上,這個數列收斂到數字
e
,也就是趨近值等於2.7182818285。)
> plot([[n, (1 + 2/n)^n] $n=1..30], x=0..30, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences154.gif)
這數列出現在收斂值趨近於7的一個極限值。(事實上精確值為![]() )
)
> plot([[n, (1 - 1/n)^n] $n=1..30], x=0..30, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences156.gif)
數列(d)也是收斂。(這時侯,精確的極限值為
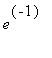 ;你開始領會到某種模式了嗎?)
;你開始領會到某種模式了嗎?)
> plot([[n, sqrt(n+1) - sqrt(n)] $n=1..30], x=0..30, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences158.gif)
數列(e)收斂到0。這是一個有趣的例題:數列中的一般項為兩個極大值的差距(假如n非常大時),它們各別計算後的值不是
![]() 或
或
![]() ,而是它們的差距;而且差距確實趨近於0。在下個例子中,將會展示出當差距趨近於0時並不總是可以明顯觀察出的。
,而是它們的差距;而且差距確實趨近於0。在下個例子中,將會展示出當差距趨近於0時並不總是可以明顯觀察出的。
> plot([[n, sqrt(n^2 + n) - n] $n=1..30], x=0..30, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences162.gif)
在這個例子中,我們再一次有這兩個極大數的差距。一個合理的趨近將了解到這極限會被指定,假如n非常大,則
![]() 會比n大的多,所以我們在平方根下應該忽略n項。這會表示出一般項應該看起來像
會比n大的多,所以我們在平方根下應該忽略n項。這會表示出一般項應該看起來像
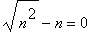 (對n值很大時)。當你從圖看到,this
(對n值很大時)。當你從圖看到,this
argument is wrong! 事實上,這數列收斂到1/2。(這個論據的解譯在Stewart的12.11節中: 二項式級數。)
> plot([[n, sin(n)] $n=1..30], x=0..30, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences169.gif)
事實上,這個數列嚴格來說是全部最難了解的,假如它沒有收斂必然可以從圖上看出。(事實上這就是答案。)似乎沒有從任何模式發展出來,然而,但是卻明顯的推算出是發散。我們能試著繪出數列中的少數項:
> plot([[n, sin(n)] $n=1..100], x=0..100, style=point);
![[Maple Plot]](L14-sequences1.files/L14-sequences170.gif)
有畫出很多點,但是仍然沒有什麼明顯的讓我們肯定它發散。事實上,這數列從沒有在任何"簡單"的表示方式中安頓下來,一直在兩個值間跳動:不論你畫了多少點,這圖片還是看起來像上面那個一樣。
當然,Maple 能以代數式地計算出極限:> limit(n/(n+1), n=infinity);
![]()
>
使用limit 指令去驗證你在問題2得到的結果。在每一個數列上使用它,甚至你認為它是發散的,如此一來你可以看到Maple如何說明這極限不存在。
解: 這是Maple照順序所計算出的七個極限 。> limit((-1)^n, n=infinity);
![]()
我們在問題2中看到這數列在1跟-1中前後跳躍,所以它沒有極限。
Maple給這”limit”一個範圍: 在1跟-1間。由於Maple
沒有給這極限單一數字,你可以從這極限的輸出推斷出,如同在課堂上所定義的,不存在。
> limit((1 + 1/n)^n, n=infinity);
![]()
它看來似乎 Maple 意識到數列跟數字 e 的關系 。還有什麼變化呢?
> limit((1 + 2/n)^n, n=infinity);
![]()
> limit((1 - 1/n)^n, n=infinity);
![]()
嗯…在一般模式下如何?(只是在例子中 x 在工作單上在別處被給定一個值,讓我們先看個例子)
> x := 'x';
![]()
> limit((1 + x/n)^n, n=infinity);
![]()
有趣地!顯然地,指數函數能被計算出一個數列中的極限值。
> limit(sqrt(n+1) - sqrt(n), n=infinity);
![]()
> limit(sqrt(n^2 + n) - n, n=infinity);
![]()
這兩個我們在問題2看到的極限是前後一致的。
> limit(sin(n), n=infinity);
![]()
當在第一個數列中,Maple 藉由給一個範圍說明了這數列不是收斂。
>
>
注意: 在這個工作單中,嚴格來說我們還沒有討論到極限的定義,至於這將定義在Stewart的580頁中。你將會預料知道這個定義,而且能使用它去表示出簡單極限的存在。