• 靠近0的近似值
• 非0點的近似值
• 泰勒指令

微積分2

 22課: 以泰勒級數去趨近一般函數

以前的課程中,我們可以看到利用多項式正確的求出sine和cosine函數靠近0的近似值。 在這個工作單中, 我們將看到能夠用這個相同的方法來接近其他的函數, 以及其他點的近似值

靠近 0 的近似值

> restart;

回憶之前這個方法是如何做到:我們找到函數靠近0的近似值，然後從原函數去減掉這個近似值，除以x的冪次方，觀察當x逼近0時，差多快逼近0。

> f := x -> sqrt(1 + x);

> plot(f, -1..1);

由於 f(0)=1, 所以我們的第一個近似值應該是常數函數(0次方多項式)1:

> p0 := x -> 1;

> limit(f(x) - p0(x), x=0);

如預期，當x趨近0，差也趨近0，我們的近似值令人滿意，但是多快呢?

> limit((f(x) - p0(x))/x, x=0);

這個極限顯示當 x 很小時f(x) - p0(x)看起來像 x / 2 , 所以我們的下一個估計值是 p0 (x) + x / 2 : 

> p1 := x -> 1 + (1/2)*x;

在進一步計算之前，讓我們來畫出原函數f 與線性近似 pl

> plot({f,p1}, -1..1);

觀察到這個線性近似只是函數  f  圖在x=0的切線而已。

> limit((f(x) - p1(x))/x, x=0);

> limit((f(x) - p1(x))/x^2, x=0);

這些極限顯示出我們已經改善這個近似值，和告訴我們下一項應是多少。

我們可以多次重覆這個步驟直到我們滿意。這裡有一些步驟。

> p2 := x -> 1 + (1/2)*x - (1/8)*x^2;

> limit((f(x) - p2(x))/x^3, x=0);

> p3 := x -> p2(x) + (1/16)*x^3;

> limit((f(x) - p3(x))/x^4, x=0);

> p4 := x -> p3(x) - (5/128)*x^4;

> p4(x);

這方法到底有多好?

> plot({f,p2,p4}, -1..1);

關於我們選擇的這個函數f沒有任何特別:這個方法對於任何合理的函數皆適用。在統計學上這裡有一個蠻重要的(它習慣於用來描述一般所謂的 常態分佈 )

> g := x -> exp(-x^2/2);

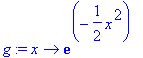
> plot(g, -4..4, 0..2);

當 x=0時, g(x)=1，所以它將會是我們第一個近似值。

> q0 := x -> 1;

> limit(g(x) - q0(x), x=0);

> limit((g(x) - q0(x))/x, x=0);

> limit((g(x) - q0(x))/x^2, x=0);

這些極限顯示常數1也是線性近似，從g 函數圖可以清楚看出。二次近似增加了新的一項。

> q2 := x -> q0(x) - (1/2)*x^2;

> q2(x);

事實上，在靠近0，g 在近似上只有x的偶次方(為什麼?)。在下面我們將利用這個事實來避免一些不必要的計算。

> limit((g(x) - q2(x))/x^4, x=0);

> q4 := x -> q2(x) + (1/8)*x^4;

> limit((g(x) - q4(x))/x^6, x=0);

> q6 := x -> q4(x) - (1/48)*x^6; q6(x);

> plot({g,q6}, -4..4, -2..2);

非 0 點的近似值

> restart;

從上面的例子發現，在0附近我們得到不錯的近似值，但是其它點就不是了。例如，假設我們想要求 在x=3的近似值，當然，在x=3時這式子確實值等於2，所以這應該為我們第一個近似值。

> f := x -> sqrt(1 + x);

> p0 := x -> 2;

下一個近似值是多少?我們想要知道當x→0時， f(x)-2接近0有多快，所以我們需要用其它較簡單趨近於0的式子比較它。當我們估計靠近0的值時，我們用它來與x的次方比較。現在我們做的是接近x=3，所以x的次方當然不接近0---但是(x-3)的次方會!

> limit(f(x) - p0(x), x=3);

> limit((f(x) - p0(x))/x, x=3);

> limit((f(x) - p0(x))/(x-3), x=3);

> p1 := x -> p0(x) + (1/4)*(x-3);

不幸地，Maple 堅持簡化一些多項式的近似值;在往後可以看到如何強迫它寫成(x-3)的次方。然而它已經寫了，雖然，我們應該可以觀察到這線性近似值為這切線:

> plot({f,p1}, -1..5);

我們可以繼續使用和以一般的方法建構高階近似式。

> limit((f(x) - p1(x))/(x-3)^2, x=3);

> p2 := x -> p1(x) - (1/64)*(x-3)^2;

> limit((f(x) - p2(x))/(x-3)^3, x=3);

> p3 := x -> p2(x) + (1/512)*(x-3)^3;

> limit((f(x) - p3(x))/(x-3)^4, x=3);

> p4 := x -> p3(x) - (5/16384)*(x-3)^4; p4(x);

> plot({f,p4}, -1..5);

這裡有其它函數為靠近x=-2的近似值。係數不是非常好，但是你可以從這點發現這個方式仍然適用。(如果你用十進位，你當然可以利用evalf,但是你必需要確定首先計算的為”精確近似值”與僅在程序的結尾使用evalf 這個指令。)

> g := x -> exp(-x^2/2);

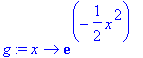
> q0 := x -> g(-2); q0(x);

> limit(g(x) - q0(x), x=-2);

> l1 := limit((g(x) - q0(x))/(x + 2), x=-2);

注意這個近似值將會為 (x-(-2))=(x+2)的次方。

> q1 := x -> q0(x) + l1*(x+2); q1(x);

和往常一樣，線性近似給我們一切線:

> plot({g,q1}, -4..0);

> limit((g(x) - q1(x))/(x+2), x=-2);

> l2 := limit((g(x) - q1(x))/(x+2)^2, x=-2);

> q2 := x -> q1(x) + l2*(x+2)^2; q2(x);

> l3 := limit((g(x) - q2(x))/(x+2)^3, x=-2);

> q3 := x -> q2(x) + l3*(x+2)^3; q3(x);

> l4 := limit((g(x) - q3(x))/(x+2)^4, x=-2);

> q4 := x -> q3(x) + l4*(x+2)^4; q4(x);

> plot({g,q4}, -4..0, thickness=2);

>

  Taylor 指令

既然我們已經發現到任何函數在任何點上如何產生這些近似多項式, 是承認Maple有內在做計算的指令的時候。 我們產生的多項式叫做泰勒多項式, 並且指令taylor將產生它們。 為了使用這個指令, 你必須給一個要展開的式子,要展開的點和所需要展開式的階數。  (Maple有關於在展開式有多少項的規則，且它們不一定是所預期，但如果你要求更多項應該得到更多項數。 ) 你能夠省略最後的這個參數; 此時Maple將用它的預設Order變量來決定項數的數量。

> f := x -> sqrt(1 + x);

> taylor(f(x), x=0, 6);

> taylor(f(x), x=0, 12);

> taylor(f(x), x=0);

> taylor(f(x), x=3);

> g := x -> exp(-x^2/2);

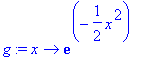
> taylor(g(x), x=0);

> taylor(g(x), x=-2);

注意這些與我們之前工作單上所產生的數列是相同的。這裡有一 些數列為你應該已經熟悉的。

> taylor(sin(x), x=0, 10);

> taylor(cos(x), x=0, 10);

> taylor(exp(x), x=0, 10);