![[Maple Plot]](L24-conicSections%20.files/L24-conicSections1.gif)
第 24 課: 圓錐剖面
我們以圓錐剖面的幾何定義開始。 之後, 我們將使用圓錐剖面的分析圖繪製在平面上。
對於下面的每一張圖片, 圓錐斷面是錐形與平面的交集。 以滑鼠抓取圖形並轉動可以從很多點觀察相交的圖。> restart: with(student):with(plottools): with(plots):
注意,名字的變化已經重新定義過了
圓
> up :=
cone([.3,0,-1],1,2,color=blue):
down := cone([.3,0,-1],1,-2,color=blue):
circlePlane := plot3d(0, x=-3..1.5, y=-1..1, color=green, style=patchnogrid):
display([circlePlane,up,down], scaling=constrained, orientation=[140,70], style=wireframe);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections1.gif)
橢圓
>ellipsePlane :=
plot3d(.75*x, x=-3..1.5, y=-1..1, color=green, style=patchnogrid):
display([ellipsePlane, up,down], scaling=constrained, orientation=[140,70],
style=wireframe);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections2.gif)
拋物線
> parabolaPlane :=
plot3d(4*x, x=-.75..(.25), y=-1..1, color=green, style=patchnogrid):
display([parabolaPlane, up,down], scaling=constrained, orientation=[140,70],
style=wireframe);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections3.gif)
雙曲線
> HyperbolaPlane :=
implicitplot3d(x=0, x=-.6..(.2), y=-1..1, z=-3..1,color=green, style=patchnogrid):
display([HyperbolaPlane, up,down], scaling=constrained, orientation=[140,70],
style=wireframe);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections4.gif)
例子 1 .
考慮下面這圓錐。 首先嘗試確認他們。 然後, 透過繪製圖形確認你的猜測。a) 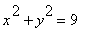
b) ![]()
c) 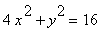
d) 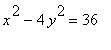
e) 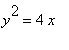
f) 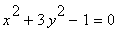
g) 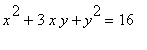
h) 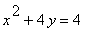
在每一種情況下, 敘述所獲得與特徵一致的圓錐。
圓的特徵= 圓心和半徑
橢圓的特徵 = 中心, 焦點 , 頂點
拋物線的特徵= 頂點, 準線 , 焦點
雙曲線的特徵= 中心, 焦點 , 頂點, 漸近線
a ) 圖形是一個圓
中心在 ( 0,0 )
半徑 = 3
> implicitplot( x^2 + y^2 = 9, x = -10..10, y = -10..10, scaling=constrained, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections13.gif)
B ) 圖表是轉動的雙曲線。
> implicitplot(x*y = -4, x = -10..10, y = -10..10, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections14.gif)
c ) 圖形是一橢圓
中心 (0,0)
焦點: (0, +- .
![]() )
)
主軸頂點 : ( 0 , + - 4 )
副軸頂點 vertices : ( + - 2 , 0 ) 。
> implicitplot(4* x^2 + y^2 = 16, x = -10..10, y = -10..10, grid=[50,50]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections16.gif)
d) 圖形是雙曲線
中心(0,0)
頂點: (+- 6, 0)
焦點( +- .
![]() ,
0)
,
0)
漸近線: y = +- .
![]()
> implicitplot(x^2 - 4* y^2 = 36, x= -10..10, y = -10..10, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections19.gif)
e ) 圖表是拋物線。
頂點: (0,0) .
焦點: (1,0) .
準線: x = -1 .
> implicitplot(y^2 = 4*x, x = -10..10, y = -10..10, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections20.gif)
f) 圖形是橢圓 。
中心: (0,0) .
焦點: ( +- .
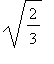 ,
0)
,
0)
主軸頂點 : ( + - 1,0 )
副軸頂點 vertices : ( 0 + - 。
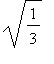 )
)
> implicitplot(x^2 + 3* y^2 - 1 = 0, x = -1..1, y = -1..1, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections23.gif)
g) 圖形是轉動的雙曲線
> implicitplot(x^2 + 3*x * y + y^2 = 16, x = -10..10, y = -10..10, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections24.gif)
h) 圖表是拋物線
頂點: (0,1) .
焦點: (0,0) .
準線: y = 2 .
> implicitplot(x^2 + 4*y = 4, x = -3..3, y = -3..3, grid=[40,40]);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections25.gif)
> completesquare(x^2 + y^2 - 2*x + 2*y + 2 = 0,x);
![]()
> completesquare(%,y);
![]()
解為一個點: ( 1 , - 1 )
>
例子 2 .
寫一個經過 ( 0,0 ) , (-4,0) 和 ( 0,6 )的圓等式,決定圓的中心和半徑。
> solve({f=0, 16 - 4*d + f =0, 36 + 6*e + f = 0},{d,e,f});
![]()
> solve({f=0, 16 - 4*d + f =0, 36 + 6*e + f = 0},{d,e,f});
![]()
因此, 圓心是:(-2,3) 和半徑是
![]() .
.
> completesquare(x^2 + y^2 + 4*x - 6*y = 0, x);
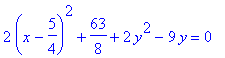
標準 形式: 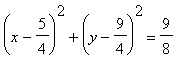 .
.
中心: ![]()
半徑: 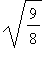
a)
我們使用: 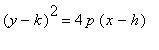
p = |3 - (-5)| = 8
h = 3, k = -2
等式是: 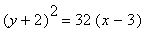
頂點是(3,-2) .
準線是: x= - 5 。
焦點是: (11,-2) .
> A:= implicitplot(y^2 = 20 * x, x = -10..10, y = -10..10):
> C:= textplot([-7,7,'directrix'], color = blue):
> E:= textplot([5.5,-2,'focus'], color = blue):
> B:= plot([-5,t, t = -10..10], color = blue):
> DD:= pointplot([11,-2]):
> display({A,B,C,E,DD});
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections37.gif)
> completesquare(%,y);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections38.gif)
例子 3 .
寫橢圓等式的標準形式和決定它的中心, 頂點 , 焦點 , 和共同頂點 。
用焦點繪製這橢圓。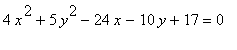
> completesquare(%,x);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections40.gif)
標準形式: 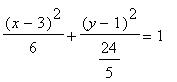
中心: (3,1)
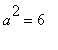 和
和 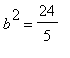 用
用 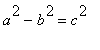 而獲得:
而獲得: 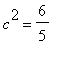
主軸頂點:
(3 +- . ![]() ,1)
,1)
次要軸頂點:(3, 1 +- . 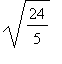 )
)
焦點:( 3 +- . 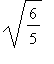 ,1).
,1).
> A:= implicitplot(4 * x^2 + 5*y^2 - 24*x - 10*y + 17 = 0, x =-1..6 ,y = -3..4):
> C:= pointplot([3 -1.095445115, 1]):
例子 4 .
寫雙曲線等式的標準形式和決定它的中心, 頂點 , 和 焦點 。
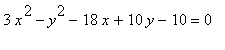
> completesquare(%,x);
標準形式: 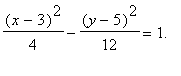
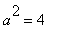 ,
和
,
和 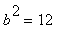 ,
求得
,
求得 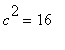 .
.
頂點: (3 +-2,5) .
焦點: (3 +- 4,5) .
中心: (3,5) .
漸近線: y = +- 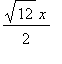 .
.
> f:= x -> 5 + 1.732050808 * (x-3) ;
![]()
> A:= implicitplot((x-3)^2/4-(y-5)^2/12
= 1, x = -10..12, y = -20..20):
B:= pointplot([7,5]):
> E:= plot(f(x), x = -10..10, color= blue):
> display({A,B,C,E,F});
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections56.gif)
例子 5 .
使用點 ( 0,0 ) , (-4,0), ( 0,6 ) 和一般等式 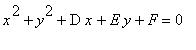
我們 獲得:
F = 0
16 - 4D + F = 0
36 + 6E + F = 0.
圓的等式是:
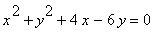 .
.
> completesquare(%,y);
例子 6 .
寫出有已知特徵的拋物線的等式。 用焦點和準線畫每一個拋物線。 在圖形上標明焦點和準線 。
a ) 頂點 ( 3 , - 2 ) 和準線x = - 5 。
b ) 經過 ( 5,10 ) , 頂點在原點, 且軸是x 軸。> A:= implicitplot((y+2)^2 = 32*(x-3), x = -10..12, y = -20..20):
> C:= textplot([-7,7,'directrix'], color = blue):
> E:= textplot([11.5,-5,'focus'], color = blue):
c
) 我們使用 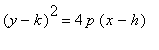 ,頂點是
( 0,0 ) 隱含h = 0 和k = 0 。
,頂點是
( 0,0 ) 隱含h = 0 和k = 0 。
因為 ( 5,10 ) 在圖形上我們有:
100 = 4 p 5 = 20 p 或者 p = 5.
等式是這樣: 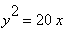 .
.
頂點是: (0,0) .
焦點是: (5,0) .
準線是: x = - 5 。
> B:= plot([-5,t,t = -10..10], color = blue):
> DD:= pointplot([5,0] ):
> display({A,B,C,DD,E});
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections61.gif)
例子 7 .
寫拋物線等式的標準形式和決定它的頂點,
焦點, 準線。
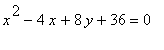
> completesquare(x^2 -4*x + 8*y + 36 = 0,x);
![]()
標準形式: 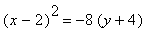
頂點: (2,-4) .
焦點: (2,-6) .
準線: y = -2 .
> A:= implicitplot(x^2-4*x+8*y+36 = 0, x = -10..12, y = -20..20):B:= plot([t,-2,t = -10..10], color = blue):
> DD:= pointplot([2,-6] ):
> display({A,B,C,DD,E});
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections65.gif)
> completesquare(4*x^2 + 5*y^2 - 24*x - 10*y + 17 = 0, y);
![]()
> (%)/24;
![]()
> evalf(sqrt(6/5));
![]()
> B:= pointplot([3 +1.095445115 , 1] ):
> display({A,B,C});
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections69.gif)
> completesquare(3*x^2 - y^2 - 18*x + 10*y - 10 = 0,y);
![]()
> (%)/12;
![]()
> evalf(sqrt(12)/2);
![]()
> g:= x -> 5 -1.732050808 * (x - 3) ;
![]()
> A:=implicitplot(3*x^2 - y^2 - 18*x + 10*y - 10 = 0, x = -6..10, y = -10..10, grid=[40,40]):
> C:= pointplot([-1,5] ):
> F:= plot(g(x), x = -10..10, color= blue):
> display(A,C,F);
![[Maple Plot]](L24-conicSections%20.files/L24-conicSections74.gif)
>