, 
, t 
![[a, b]](parametricArcLength.files/L26-parametricArcLength3.gif){kind=small}
來描述
第 26 課:
參數弧長
在這個工作單中, 我們將用積分的方法來計算平面參數曲線的長度。 以相同的方法將可求得3維的曲線的長度,
但是, 我們將不考慮此延伸。 設想我們被給了一個參數曲線, 以等式
,
, t
來描述
> f := t-> t^2 ; g := t-> t^3 - 3*t ;
> plot([f(t), g(t), t=-2..2]);
![[Maple Plot]](parametricArcLength.files/L26-parametricArcLength6.gif)
我們以端點
, 
, ... ,
將這參數
在區間![[a, b]](parametricArcLength.files/L26-parametricArcLength7.gif){kind=small}
分成n等分 ， 然後畫出連接相應於原始曲線上的點的片斷-線性的曲線
。 它顯示出, 我們能用先前計算弧長的副程式 pl 去計算它。 我們只必須各別地對應用 pl 到 
和 
。
> pl := proc(f,a,b,n)
> local u,v,k;
> k := 1 + floor(n*(x-a)/(b-a));
> u := a + (k-1)*(b-a)/n;
> v := a + k*(b-a)/n;
> unapply(f(u) + (f(v) - f(u))/(v-u)*(x-u), x);
> end proc:
> plf := pl(f,-2,2,6):
> plg := pl(g,-2,2,6):
> plot({[f(t),g(t),t=-2..2], [plf(t),plg(t),t=-2..2]}, thickness=2);
![[Maple Plot]](parametricArcLength.files/L26-parametricArcLength14.gif)
(當
和
被定義時，我們抑制了這輸出;它不是很有趣的。)
計算 片 斷- 線性曲線的長度是 容易的。 一個典型片斷連結點( 
, 
) 和 ( . 
, 
) ,
所以可以從距離公式去計算它的長度。加這些長度得到這個公式
.
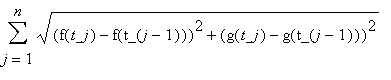已知函數 
和 
, 參數區間 ![[a, b]](parametricArcLength.files/L26-parametricArcLength24.gif){kind=small}
和子區間的數目，下面的程式計算這個公式,
> approxlen := proc(f,g,a,b,n)
local l;
l := (b-a)/n;
sum( sqrt( (f(a+j*l) - f(a+(j-1)*l))^2
+ (g(a+j*l) - g(a+(j-1)*l))^2 ), j=1..n);
end proc:
如平常一樣, Maple將正確地計算出答案, 包括平方根, 所以可以很方便的要求用小數接近。
> evalf(approxlen(f,g,-2,2,5));
> evalf(approxlen(f,g,-2,2,10));
> evalf(approxlen(f,g,-2,2,20));
> evalf(approxlen(f,g,-2,2,50));
> evalf(approxlen(f,g,-2,2,100));
我們看見一個熟悉的模式:如當子區間的數目增加, 這些用片斷-線性長度的近似值接近一個固定的值，它明顯地是原始曲線的真實長度。
>
以精確度於0.01之內,用片斷-線性近似值找出上述曲線迴圈的長度。
(暗示: 曲線本身的交點，t 的兩個值為何?).
解答: 當 
曲線交於
x- 軸 且當
時再生交點時，當時兩個是在
x=3 在 
的這兩個值之間曲線的長度能夠估計
使用 approxlen :
> evalf(approxlen(f,g,-sqrt(3),sqrt(3),5));
> evalf(approxlen(f,g,-sqrt(3),sqrt(3),10));
> evalf(approxlen(f,g,-sqrt(3),sqrt(3),50));
> evalf(approxlen(f,g,-sqrt(3),sqrt(3),100));
雖然我們應該儘可能試試大量的子區間去確定第二位小數點將仍維持穩定，我們也許能夠認定長度是 10.73，0.01之內的精確。
>
>
繪製極曲線 
，
以之寫成一參數曲線，求
和 
之間的長度。
解答: 如一極曲線, 我們的曲線有等式 
, 
.
> f1 := theta-> theta*cos(theta) ;
>
> g1 := theta-> theta*sin(theta) ;
>
> plot([f1(theta), g1(theta), theta=0..2*Pi]);
![[Maple Plot]](parametricArcLength.files/L26-parametricArcLength47.gif)
> evalf(approxlen(f1,g1,0,2*Pi,50));
> evalf(approxlen(f1,g1,0,2*Pi,100));
> evalf(approxlen(f1,g1,0,2*Pi,500));
曲線的長度被估計約 21.25 。
>
當我們想要精確找出的弧長時利用Maple的次方以及以數字表示的方式的approxlen既可以找到我們所需要的。
經常以這種數值程式是得到弧長的唯一實用方法，但是，要把已知曲線精確長度的積分式寫下來是可能的。
(實際上，對多數曲線，積分將必須以數值計算。)如同在課堂上所解釋，Mean Value Theorem導出積分式。
.
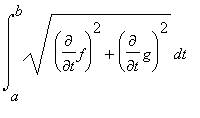下面的程式傳回這積分值。 因為許多弧長的積分不可以符號運算求得。 arclength 傳回的積分值是沒有被計算出的 ;它的值需使用 evalf 去得到小數點近似值。
> arclength
:= proc(f,g,a,b)
Int(sqrt(diff(f(t),t)^2 + diff(g(t),t)^2), t=a..b);
end proc:
對於我們使用的例子，我們能夠確認積分公式符合我們從片斷-線性的估計值得到弧長。
> f := t-> t^2 ; g := t-> t^3 - 3*t ;
> evalf(arclength(f,g,-2,2));
證實這積分公式是符合問題1和問題2用片斷-線性近似所得到的值。
解答 :
> evalf(arclength(f,g,-sqrt(3),sqrt(3)));
> evalf(arclength(f1,g1,0,2*Pi));
這兩個值符合我們在問題1和2所得到的近似值，至少在最初的若干小數。假如我們在問題1和2使用更多的間距，我們當然
就會得到更好的值。