• 介紹 
• 程式碼 
• Examples 

梯形規則

Sylvain Muise 

<smuise@student.math.uwaterloo.ca>

介紹 

梯形規則是許多估計方法中的一種定積分。 由左-點和右-點之間的平均值找到它，其定義如下:

左端點規則: =

右端點規則: =

其中 和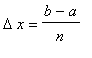  

由於所產生的多邊形的形狀所以叫它作梯形規則。 這maple應用問題使用了圖表及動畫展示梯形規則。

程式碼

> restart:

> leftGraph := proc(f, a, b, n)
local dX, boxes, i, x0, x1, graph:
dX := (b-a)/n:
boxes := []:
for i from 1 to n do
x0 := a+(i-1) * dX:
x1 := a + i * dX:
boxes := [op(boxes), plottools[polygon]([[x0, 0], [x0,f(x0)],[x1,f(x0)],[x1,0]], color=cyan)]:
end do:
graph := plot(f(x),x=a..b):
plots[display]([graph,seq(boxes[i],i=1..n)], axes=normal)
end proc:

> rightGraph := proc(f, a, b, n)
local dX, boxes, i, x0, x1, graph:
dX := (b-a)/n:
boxes := []:
for i from 1 to n do
x0 := a+(i-1) * dX:
x1 := a + i * dX:
boxes := [op(boxes), plottools[polygon]([[x0,0],[x0,f(x1)], [x1, f(x1)], [x1, 0]], color=cyan)]:
end do:
graph := plot(f(x), x=a..b):
plots[display]([graph, seq(boxes[i],i=1..n)], axes=normal)
end proc:

> trapGraph := proc(f, a, b, n)
local dX, traps, i, x0, x1, graph:
dX := (b - a) /n:
traps := []:
for i from 1 to n do
x0 := a + (i-1) * dX:
x1 := a + i * dX:
traps := [op(traps), plottools[polygon]([[x0,0],[x0,f(x0)],[x1, f(x1)], [x1, 0]], color=cyan)]:
end do:
graph := plot(f(x),x=a..b):
plots[display]([graph, seq(traps[i], i=1..n)], axes=normal)
end proc:

> animateTraps := proc(f, a, b, initN, finalN)
local i, animations, temp:
if initN <= finalN then
for i from initN to finalN do
animations[i] := trapGraph(f,a, b, i):
end do:
temp := initN:
temp2 := finalN:
elif initN > finalN then
temp := initN:
for i from finalN to initN do
animations[temp] := trapGraph(f,a,b,i):
temp := temp - 1:
end do:
temp := finalN:
temp2 := initN:
end if:
plots[display](seq(animations[i],i=temp..temp2),insequence=true, axes=normal)
end proc:

 注意`temp2` 隱含地宣佈區域變數是對副程式 `animateTraps` 。

Examples

首先, 定義一個函數。 Ex: f := x -> sin(x);
前三個函數, leftGraph , rightGraph , 和 trapGraph , 顯示出函數影像和相對應的近似值
Parameters: ????Graph(f, a, b, n)
f:這個函數
a:接近積分的下限
b:接近積分的上限
n: 用來接近積分的梯形數目

第二個函數, animateTraps , 隨著改變n的值而顯示出梯形和函數的動態圖。
參數: animateTraps(f, a, b, initN, finalN)
f: 這個函數
a: 接近積分的下限
b: 接近積分的上限
initN : 一開始用來接近積分的梯形數目
finalN : 最後用來接近這個積分的梯形數目
Examples

> f := x -> sin(x);

> leftGraph(f, 0, 4*Pi, 20);

>rightGraph (f, 0, 4*Pi, 20);

 

>trapGraph (f, 0, 4*Pi, 20);

>animateTraps (f, 0, 4*Pi, 1, 20);

>animateTraps(f, 0, 4*Pi, 20, 1);

>g := x -> x^3:

>leftGraph(g, -10, 10, 5);

>rightGraph(g, -10, 10, 5);

>trapGraph(g, -10, 10, 5);

>animateTraps(g, -10, 10, 1, 20);

>trapGraph(h, -2, 2, 5);

>animateTraps(h, -2,2,1, 30);